深入解析期权定价的数学模型和方法详细案例分析与应用

说在前面

主题介绍：本文将深入解析期权定价的数学模型和方法，通过详细案例分析和具体应用，帮助读者全面理解这一领域的重要概念和方法。

重要性说明：期权在金融市场中扮演着重要角色，其定价直接影响市场操作和投资策略。因此，理解期权定价的数学模型和方法，对于投资者和金融从业者都极为重要。

预期内容概述：文章将介绍期权定价的基本概念和历史发展，详细解读几种主要的期权定价模型，同时结合案例展示这些模型的现实应用，并提供相关实用的小技巧和常见问题解答。

期权定价的基本概念和背景

定义和基本概念：期权是一种金融衍生工具，它赋予买方在未来某一特定日期以特定价格买入或卖出标的资产的权利。期权定价涉及数学模型，这些模型旨在评估期权的公允市场价值。

历史和发展：期权定价的理论发展始于20世纪70年代，费希尔·布莱克（Fisher Black）和迈伦·斯科尔斯（Myron Scholes）在1973年提出了著名的布莱克-斯科尔斯模型（Black-Scholes），这标志着期权定价理论进入了一个新的阶段。随后，其他模型如Cox-Ross-Rubinstein二叉树模型也相继提出，并得到了广泛应用和发展。

期权定价的数学模型和方法

布莱克-斯科尔斯模型 (Black-Scholes Model)

布莱克-斯科尔斯模型是期权定价的基石，它使用了随机微分方程和无风险对冲的概念来计算期权价格。该模型假设标的资产价格服从几何布朗运动，并且市场没有交易成本和税收，且可以连续交易。

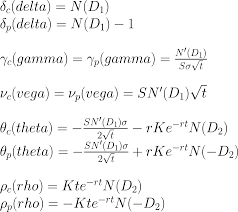
Cox-Ross-Rubinstein 二叉树模型 (CRR Binomial Model)

CRR二叉树模型是一种离散时间模型，通过构建树状结构，将期权到期日之前的价格波动情况离散化。其核心思路是将标的资产价格在每个时间节点上可能的涨跌离散为两个结果，从而逐步逼近期权的理论价格。

[插图：CRR二叉树模型结构图]

蒙特卡洛模拟 (Monte Carlo Simulation)

蒙特卡洛模拟方法利用随机数生成和数值计算技巧，通过大量重复模拟标的资产价格过程来估计期权价格。这种方法在进行复杂期权定价和风险管理时尤其有用。

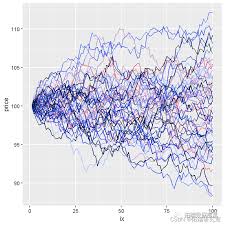
Heston 模型

Heston模型是一个随机波动率模型，假设标的资产价格和波动率都服从随机过程。该模型可以更好地捕捉标的资产价格波动的不对称性和非恒定性。

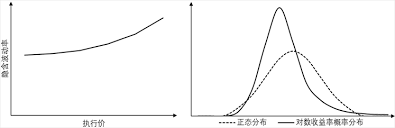
详细案例分析与应用

案例一：使用Black-Scholes模型定价欧式看涨期权

假设一个标的股票目前价格为$100，执行价格为$105，年化无风险利率为5%，波动率为20%，到期时间为一年。使用Black-Scholes模型可以计算出该看涨期权的公允价格。

步骤：

• 计算d1和d2。
• 利用累计正态分布函数计算N(d1)和N(d2)。
• 代入Black-Scholes公式计算期权价格。

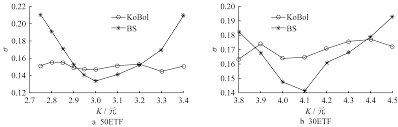
案例二：使用蒙特卡洛模拟定价复杂期权

假设一个亚洲期权，其特点是期权价格取决于标的资产价格在整个有效期内的平均值。使用蒙特卡洛模拟方法，可以通过大量模拟计算得出这一期权的价格。

步骤：

• 生成大量标的资产价格路径。
• 计算每条路径下的期权价格。
• 将所有路径的期权价格平均化，得到期权的估计价格。

实用Tips

• 始终选择合适的模型：不同的期权和市场条件适用不同的定价模型，了解每个模型的优缺点非常重要。
• 充分利用现有软件工具：例如MATLAB、R语言和Python等都提供了丰富的金融计算库，可以大大简化计算过程。
• 关注市场数据：定价模型依赖于市场数据，如波动率和无风险利率，时刻关注这些数据可以提高定价准确性。
• 进行敏感性分析：通过敏感性分析，可以了解期权价格对不同输入参数的敏感度，从而更好地管理风险。
• 多读多问：不断学习和问询专家意见，可以迅速提升期权定价的专业技能。

常见问题解答（FAQ）

1. 什么是隐含波动率？
   隐含波动率是指市场对期权未来波动率的预期，是通过反解期权价格公式得到的波动率指标。
2. 为什么Black-Scholes模型假设标的资产价格服从几何布朗运动？
   这是因为几何布朗运动可以很好地模拟资产价格的随机游走特性，并且其数学特性使得公式推导更加简洁。
3. 如何选择合适的期权定价模型？
   选择合适的模型主要取决于期权的类型、市场条件和定价要求。简单期权可以使用Black-Scholes模型，复杂期权可能需要蒙特卡洛模拟等方法。
4. 什么是二叉树模型的优点？
   二叉树模型的主要优点是其灵活性和直观性，可以模拟美式期权等需要在到期前行使的复杂期权。
5. 为什么要进行蒙特卡洛模拟？
   蒙特卡洛模拟方法可以处理复杂的期权定价问题，尤其是在无法使用解析方法的情况下，它通过大量随机模拟为出价提供了切实可行的解决方案。

总结

期权定价的数学模型和方法是金融学中极其重要的内容，通过本文的详细解析，我们了解了Black-Scholes模型、Cox-Ross-Rubinstein二叉树模型、蒙特卡洛模拟和Heston模型等。上述模型不仅各有优缺点，而且适用不同的市场和期权类型。希望通过本文的介绍，投资者和金融从业者能够更好地理解这些模型，并在实际应用中做出更加明智的决策。

未来，可以进一步学习这些定价方法的数学基础，以及如何使用金融软件工具来简化计算过程。同时，关注市场变化和不断进行实践，不断提高对这些工具的驾驭水平，以更好地应对复杂多变的金融市场。